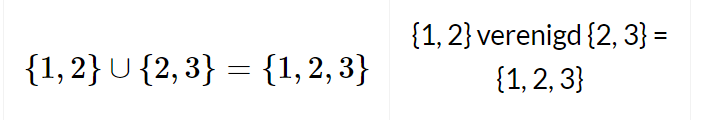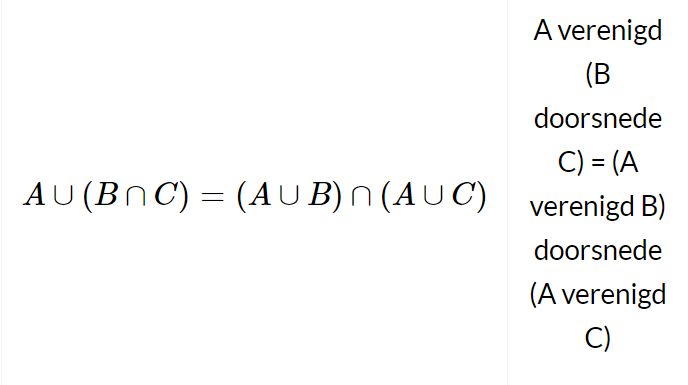Nieuwe pagina 1

Wiskundige Weetjes

Terug Nog in opbouw.

Als eerste een klein woordje over de wiskunde. Wiskunde is de universele taal dat gesproken wordt over heel de wereld zelfs in heel het universum. Wiskunde is niet iets wat de mensen hebben uitgevonden, maar dat was er, de mensen hebben het enkel een naam gegeven aan de dingen die ze zagen, voorbeeld er viel een appel op de grond, ha dat is dan 1, toen viel er nog eentje. Ha dat is dan 2, aha dus 1+1 = 2, en zo is de wiskunde gegroeid. Later was er een snuggere die graag wou weten hoeveel keer gaat de doormeter van een cirkel in de omtrek, dat hebben ze dan Pi (η) genoemd, en zo verder, tot de moeilijkst formules alles is ontstaan uit 1+1=2.
Vb. 3x3=9 computer maakt daar 3+3+3 van of in binair 11+11+11=1001. Klik hier voor Dec Bin AscII Tabel.
Een computer kan niet anders rekenen, dan enkel maar nullen en enen op te tellen zelfs de moeilijkste berekeningen worden herleid tot optellen van enen en nullen.
Dus mensen geen bang hebben van wiskunde. Het is enkel maar 1+1=2.

Deelbaarheid van getallen.

Het getal 0	Delen door nul is niet mogelijk.
Het getal 1	Ieder getal kan altijd door 1 gedeeld worden. Dit geeft terug het getal.
Het getal 2	Een getal is deelbaar door 2 als het laatste cijfer 0 of een paar getal is.
Het getal 3	Een getal is deelbaar door 3 als de som van alle cijfers deelbaar is door 3.
Het getal 4	Een getal is deelbaar door 4 als de laatste 2 cijfers deelbaar zijn door 4 of 00.
Het getal 5	Een getal is deelbaar door 5 als het laatste cijfer een 0 of 5 is.
Het getal 6	Een getal is deelbaar door 6 als het getal deelbaar is door 2 en ook door 3.
Het getal 7	Voor 7 bestaan er geen trucjes.
Het getal 8	Een getal is deelbaar door 8 als de laatst 3 cijfers deelbaar is door 8.
Het getal 9	Een getal is deelbaar door 9 als de som van alle cijfers deelbaar is door 9.
Het getal 10	Een getal is deelbaar door 10 als het laatste cijfer een 0 is.
Het getal 25	Een getal is deelbaar door 25 als de laatste 2 cijfers deelbaar zijn door 25 of 00
Het getal 100	Een getal is deelbaar door 100 als het laatste 2 cijfers 00 is.
Het getal 1000	Een getal is deelbaar door 1000 als het laatste 3 cijfers 000 is.

Spelen met Getallen.

De getallen 1 2 4 5 7 8.

We Verdubbelen	Tellen cijfers op	Tellen cijfers opnieuw op	Uitkomst
1			1
2			2
4			4
8			8
16	1+6=7		7
32	3+2=5		5
64	6+4=10	1+0=1	1
128	1+2+8=11	1+1=2	2
256	2+5+6=13	1+3=4	4
512	5+1+2=8		8
1024	1+0+2+4=7		7
2048	2+0+4+8=14	1+4=5	5

Zo kunnen we verdergaan tot in het oneindige we gaan altijd de
reeks 1 2 4 8 7 5 uitkomen.

Het getal 9 is een super getal.

9			9
18	1+8=9		9
36	3+6=9		9
72	7+2=9		9
144	1+4+4=9		9
288	2+8+8=18	1+8=	9
9 / 2 = 4,5	4+5=9		9
4,5 / 2 = 2,25	2+2+5=9		9

De getallen 3 en 6.

3			3
6			6
12	1+2=3		3
24	2+4=6		6
48	4+8=12	1+2=3	3
96	9+6=15	1+5=6	6

Zo kunnen we verdergaan tot in het oneindige we gaan altijd de
reeks 3 6 uitkomen.
Bekijk eens de getallen figuur, Is dit een bekende figuur?

Voor dat we verdergaan bekijk eerst eens de filmpjes over Basis Wiskunde.

Meetkunde.

Bereken oppervlakte Oppervlakte cilinder A = Pi x r².	Bereken Inhoud Inhoud cilinder V = Pi x r² x H.	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier
Bereken oppervlakte Stap 1: Straal r r=0.5p+(k²/8p) Stap 2: Hoek a a=2arccos(1-(p/r)) Stap 3: Oppervlakte A O=0.5r²(a-sin(a))	Bereken Inhoud Inhoud deel cilinder V = O x L	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier
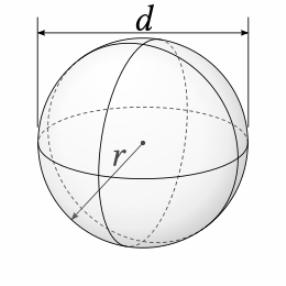Bereken oppervlakte Oppervlakte Bol O=4 x Pi x r²	Bereken Inhoud Inhoud Bol V= 4/3 x Pi x r³	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier
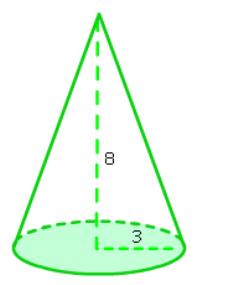Bereken oppervlakte Oppervlakte grond-vlak Kegel O = Pi x r².	Bereken Inhoud Inhoud Kegel V=1/3 x Pi x r² x H	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier
Bereken oppervlakte Oppervlakte grond-vlak Kegel O = L x B.	Bereken Inhoud Inhoud Kegel V=1/3 x L x B x H	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier
Eigenschappen Som van hoeken=180° Bereken oppervlakte O=1/2ch of O=1/2ab(sin(ab))	Stelling van Pythagoras Oppervlaktevierkant met zijde a + Oppervlaktevierkant met zijde b = Oppervlaktevierkant met zijde c Rechthoekige driehoek a² + b² = c²	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier
Berekenen Hellingpercentage Vertical/Horizontalx100 P = V / H x 100	Afgeleide Formulles V = H / 100 x P H = V x 100 / P	Small Basic Programma Downloaden. Voor deze berekeningen Klik Hier

Meer uitleg klik op: Verschillende soorten vormen en of Eigenschappen van de verschillende Vormen

Gelijke Driehoeken (congruent)

Wat moeten we hiervoor zeker kennen om tot een oplossing te komen!
Kennis 01

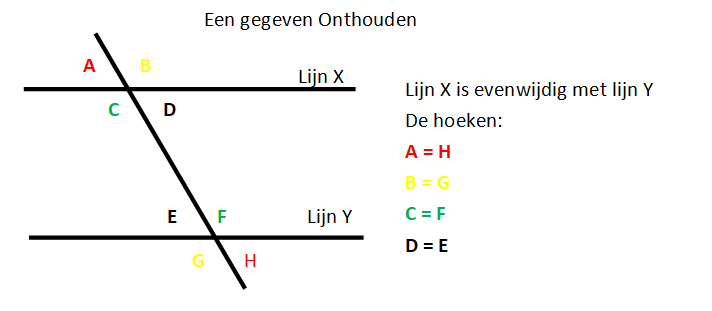
Kennis 02
Om een driehoek eenduidig te bepalen, heb je minimaal drie gegevens nodig, waarvan minstens één zijde moet zijn. Er zijn verschillende combinaties mogelijk:
- Drie zijden (ZZZ- zijde, zijde, zijde).
- Twee zijden en de ingesloten hoek (ZHZ - zijde, hoek, zijde).
- Een zijde en twee hoeken (HHZ of HZH - hoek, hoek, zijde).
- Twee zijden en een niet-ingesloten hoek (ZZH- zijde, zijde, hoek).
Dus je hebt minimaal 3 gegevens nodig, inclusief minstens 1 zijde om een driehoek uniek te bepalen.

Eerste Opgave

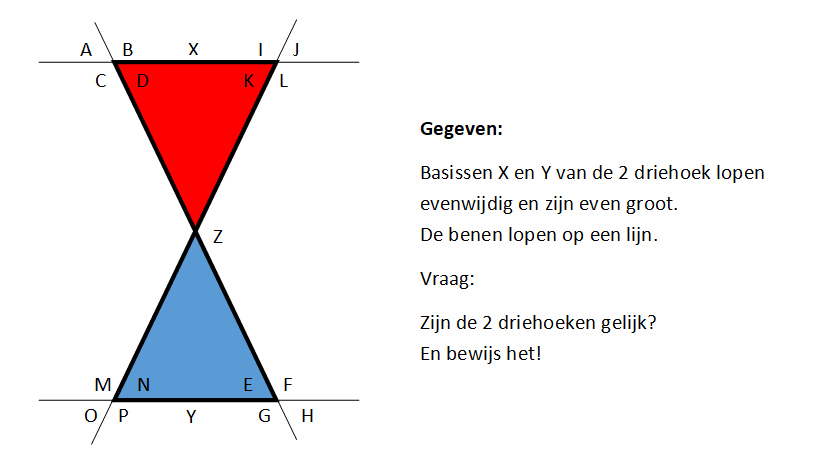
Oplossing:
Als eerst moeten we Kennis 01 goed begrijpen en onthouden dit gaan we straks toepassen bij de oplossing
Dit geld ook voor Kennis 02 hier moeten we onthouden de verschillende mogelijk heden voor het volledig bepalen van de driehoek
(ZZZ of ZHZ of HHZ of HZH of ZZH)
Dan gaan we kijken welke van de mogelijkheden in Kennis 02 we kunnen toepassen
ZZZ of ZHZ of HHZ of HZH of ZZH en indien we een van de vijf vinden voor beide driehoeken, dan zijn deze gelijk.

Een ding hebben we al gekregen, een Z (zijde) de basissen van de driehoek zijn gelijk X = Y (gegeven)
en wat we ook gekregen hebben is dat X evenwijdig loopt met Y met dit gegeven en de eigenschappen uit hoofdstuk 01 kunnen we zeggen dat de hoeken D = E en K = N, Dus we hebben HHZ voor beide driehoeken en deze zijn ook gelijk met andere woorden beide driehoeken zijn gelijk

Tweede Opgave

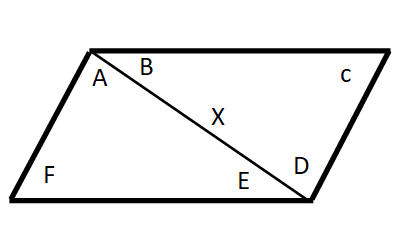
We snijden een Parallellogram van een hoek naar de tegenovergestelde hoek
nu krijgen we 2 driehoeken AEF en BCD
Vraag:
Zijn deze 2 driehoeken gelijk? Zo ja, bewijs het!
Antwoord:
JA!
Bij een Parallellogram zijn de tegenovergestelde zijden evenwijdig hierdoor kunnen zeggen dat hoek A en D gelijk zijn en B en E ook gelijk zijn (zie Kennis 01) en de zijde X is gemeenschappelijk dus ook gelijk nu hebben 2 Hoeken en 1 zijde dat gelijk is (HHZ) zie Kennis 02. De driehoeken zijn gelijk.

Derde Opgave

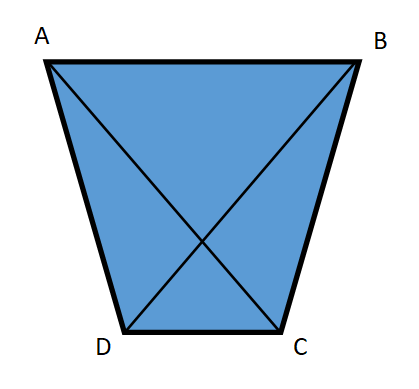
Gelijkbenig trapezium
Vraag:
Zijn de driehoeken ADC en BCD gelijk (congruent) in de gelijkbenig trapezium?
Zo ja! Bewijs het.

Als eerste gaan we kijken naar de eigenschappen van een Gelijkbenig trapezium
Twee evenwijdige zijden: Een trapezium heeft altijd twee evenwijdige zijden (de basislijnen).
Gelijke benen: De niet-evenwijdige zijden (de benen) zijn even lang.
Gelijke basishoeken: De hoeken aan de basis (waar een been en een basislijn samenkomen) zijn aan beide kanten gelijk.
Symmetrie: Een gelijkbenig trapezium heeft een spiegelsymmetrie ten opzichte van de middelloodlijn van de basislijnen.
Diagonalen even lang: De diagonalen van een gelijkbenig trapezium zijn even lang.
Antwoord
JA, en we kunnen het bewijzen, enkel door de Eigenschappen.
De zijden AD en BC zijn gelijk (Gelijke benen) nu hebben we al een Z
De Zijde DC is gemeenschappelijk nu hebben we een 2de Z
Nu nog een ingesloten hoek voor de H. En deze vinden we door de eigenschap Gelijke basishoeken Hoeken D en C zijn gelijk.
Dus nu hebben we ZHZ en de twee driehoeken zijn gelijk.

Breuken optellen, Aftrekken, vermenigvuldigen en Delen. Voor filmpjes klik hier.

Optellen	1/6+2/6 = 3/6 = 1/2 Bij gelijk noemers kunnen de tellers op geteld worden daarna kleiner maken. 1/4+3/8 = 2/8+3/8 = 5/8 Eerst noemers gelijk maken, daarna tellers optellen en kleiner maken. 2(1/3)+1(3/4) = 2(4/12)+1(9/12) = 3(13/12) = 4(1/12) 2(1/3)+1(3/4) = 7/3+7/4 = 28/12+21/12 = 49/12 = 4(1/12)
Aftrekken	2/6-1/6 = 1/6 Voor aftrekken gelden de zelfde regels als optellen.
Vermenigvuldigen	2/7x3/5 = 6/35 We Vermenigvuldigen de tellers en noemers met elkaar. 2x3/8 = 6/8 = 3/4 3/5 x 5/8 = 3/8 De gelijke cijfers tussen tellers en noemers kunnen we schrappen.
Delen	3/5 : 4/7 = 3/5 x 7/4 = 21/20 = 1(1/20) Draai tweede breuk om en Vermenigvuldig met eerste. 1(1/3) : 3(1/4) = 4/3 : 13/4 = 4/3 x 4/13 = 16/39
Met Letters	a/b x c/d = ac/bd Met Letters gelden de zelfde regels als met Cijfers a/b + c/b = ac/b a/b + c/d = ad/bd + bc/bd = ab+bc/bd x/x-1 - 2/x+3 = x(x+3)/(x-1)(x+3) - 2(x-1)/(x-1)(x+3) = x(x+3) - 2(x-1)/(x-1)(x+3) = x²+3x-2x+2/(x-1)(x+3) = x2+x+2/(x-1)(x+3) Bekijk zeker eens het filmpje over Breuken met letters samennemen, vereenvoudigen en uitdelen.

Algebra

Getallen Lijn

...

-9

-8

-7

-6

-5

-4

-3

-2

-1

...

De Regels van Algebra die Geassocieerd worden met Rekenkunde.

Volgorde van bewerkingen 1 Haakjes 2 Machtsverheffen 3 Worteltrekken 4 Vermenigvuldigen 5 Delen 6 Optellen 7 Aftrekken	9/3-5+3x4 = (9/3)-5+(3x4) = (9/3)-5+12 = 3-5+12 = (3+12)-5 = 10
Het optellen van twee negatieve getallen maakt de som negatiever	(-15)+(-3)=-18 -15-3=-18
Het aftrekken van een negatieve getal is hetzelfde als het optellen van een positieve getal	-15+3=-12
Vermenigvuldigen of delen van twee negatieve getallen geeft een positief antwoord.	(-15)x(-3)=+15
Vermenigvuldigen of delen van een positief getal en een negatief getal geeft een negatief antwoord.	(-15)x(+3)=-45 -15)/(+3)=-5
Je vermenigvuldiging kan verdeeld worden over elk van de verschillende termen die aan de vergelijking verbonden zijn	Y(X + Z) = YX + YZ
Door de noemer van een breuk te delen, zal dit hetzelfde effect hebben als het vermenigvuldigen van de teller	A/(B/C) = AC/B
De noemers moeten bij elkaar worden gevoegd, en hun sommen moeten boven de gemeen- schappelijke noemer worden geplaatst	A/C + B/C = A+B/C
Pi verhouding doormeter omtrek cirkel The golden ratio constanten Euler's constant Euler's number	µ = 3,14159... ° = 1,61803…. y = 0.57721... e = 2,71828...

Verzamelingen

Een verzameling is zo als het woord zelf zegt een groepering (Verzameling) van elementen.
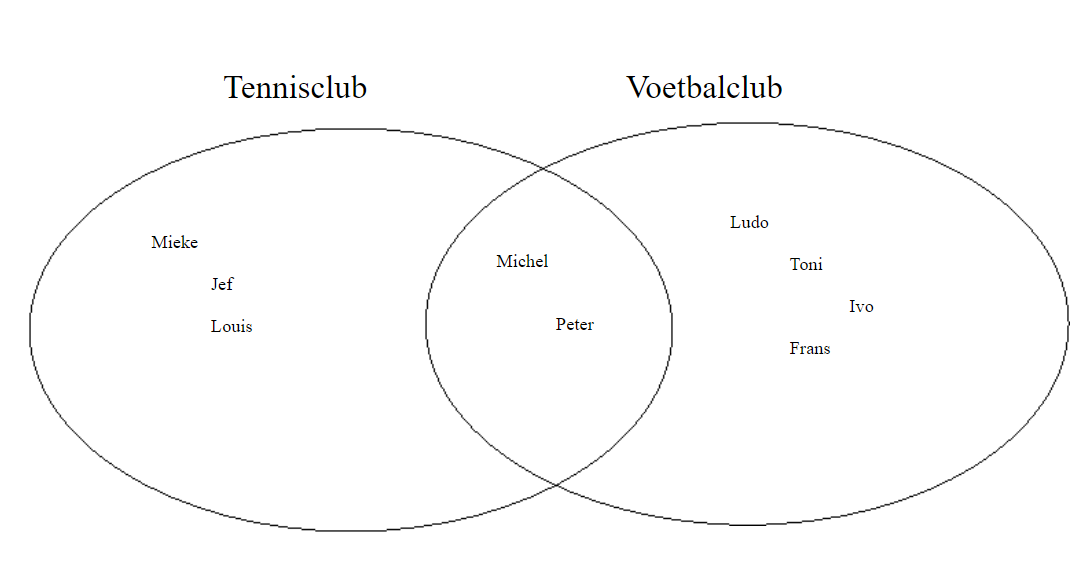
Men zou kunnen zeggen leden van een tennisclub een verzameling is, en leden van een voetbalclub is een ander verzameling.
Nu zijn er ook leden van tennisclub die ook lid van voetbalclub zijn.
Zo ziet dan de verzameling uit

Verzamelingen in de wiskunde:
In de wiskunde is ‘een veelheid van elementen, die volgens een bepaalde definitie bij elkaar horen en daardoor een geheel vormen’, oftewel, een verzameling is een collectie van verschillende objecten, elementen genoemd. De verzameling zelf wordt als een wiskundig object beschouwd. Dat wil zeggen dat je met verzamelingen berekeningen kunt maken

Nu gaan we de verschillende soorten verzamelingen beschrijven.

Doorsnede.

Vereniging.

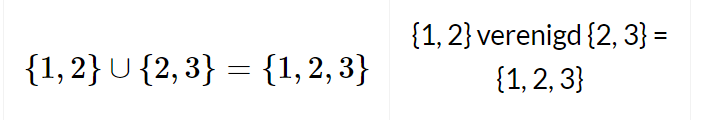
Lege verzameling.

Regel van de Morgan.

Distributiviteit.

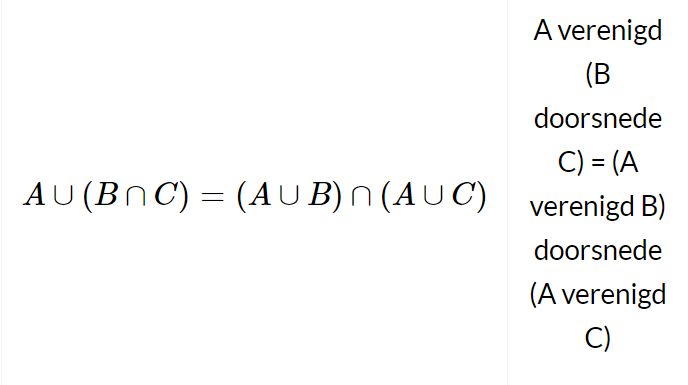
Deelverzameling.

Deelverzameling of gelijk aan.

Geen deelverzameling.

Een element van de gehele getallen

Geen element van de natuurlijke getallen.

De Sinusregel:

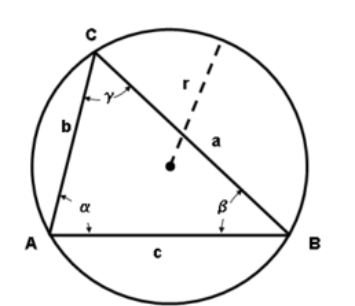
De sinusregel bepaalt dat de verhouding tussen de lengte van een zijde en de sinus van de tegenoverliggende hoek gelijk zijn aan elkaar, dus:
De sinusregel kan dus gebruikt worden om een driehoek te berekenen, indien 2 zijden en een aanliggende hoek gekend zijn. Indien je bij het berekenen van een hoek A een waarde voor sin(A) > 1 bekomt, is de driehoek niet mogelijk met de opgegeven gegevens.
Klik Hier voor Sinus Tabel.

De Cosinusregel:

De cosinusregel kan gebruikt worden voor het berekenen van een willekeurige driehoek, indien de drie zijden gekend zijn, of indien 2 zijden en de ingesloten hoek gekend zijn (in deze twee gevallen kan men de sinusregel niet gebruiken...)
Klik Hier voor Cosinus Tabel.

DE Tangensregel.

De tangensregel is een stelling uit de goniometrie die stelt dat in een willekeurige driehoek in het platte vlak met zijden
vlak met zijden a, b en c en de overstaande hoeken.
Klik Hier voor Tangens Tabel.

Alles wat je hier gezien hebt en nog veel meer vind je in de volgende filmpjes Hogere Wiskunde.

Terug